« Votre modèle Shaft_Support_1.stl de la commande n ° 15251 était
retiré de la production par l’un de nos ingénieurs d’impression 3D en raison de la conception
problèmes: épaisseur de paroi. Voir l’image ci-jointe… »
Semble familier? Si vous avez déjà eu un modèle rejeté par les ingénieurs d'impression 3D en raison de problèmes d'épaisseur de paroi, vous n'êtes pas seul. Bien qu'il s'agisse d'un problème très courant, de nombreux modélisateurs 3D peuvent ne pas savoir comment l'épaisseur de la paroi est inspectée.
Shapeways imprime quotidiennement des milliers de pièces, avec un système complet d'inspection de l'épaisseur de paroi en fonction de la conception et des matériaux.
Qu'est-ce que l'épaisseur de la paroi et pourquoi est-elle si importante dans l'impression 3D?
En examinant de plus près les coulisses pour comprendre les calculs, il est clair que de nombreux modèles 3D ont fière allure sur l'écran de l'ordinateur mais deviennent gênants pendant le processus réel d'impression 3D.
Des difficultés surviennent lorsque les modèles sont trop minces et que le scénario s'aggrave face à des matériaux et à une technologie moins avancés. Tenter d'imprimer des modèles en 3D avec des aspects minces entraînera probablement un échec de la construction, ainsi que des modèles fragiles en post-traitement, en expédition ou en utilisation finale.
Bien qu'une analyse complète de la résistance structurelle soit idéale, cela pose également un problème de calcul complexe, ce qui conduit les ingénieurs d'impression 3D à utiliser des mesures empiriques plus simplifiées avec analyse de l'épaisseur de paroi. Si le modèle a des régions qui sont plus minces qu'un certain seuil expérimental appelé épaisseur de paroi minimale, nous supposons que le modèle a une forte probabilité de rupture; par conséquent, les ingénieurs ont besoin d'outils pour voir où le modèle est trop mince.
La visualisation de l'épaisseur des parois dans l'impression 3D nécessite une approche simple
Prenons l'exemple d'un petit vase (illustré ci-dessous en coupe transversale). Le vase a une très petite ouverture, et lorsque nous l'examinons de l'extérieur, nous n'avons aucune idée qu'il a deux points offensants avec des parois très minces.
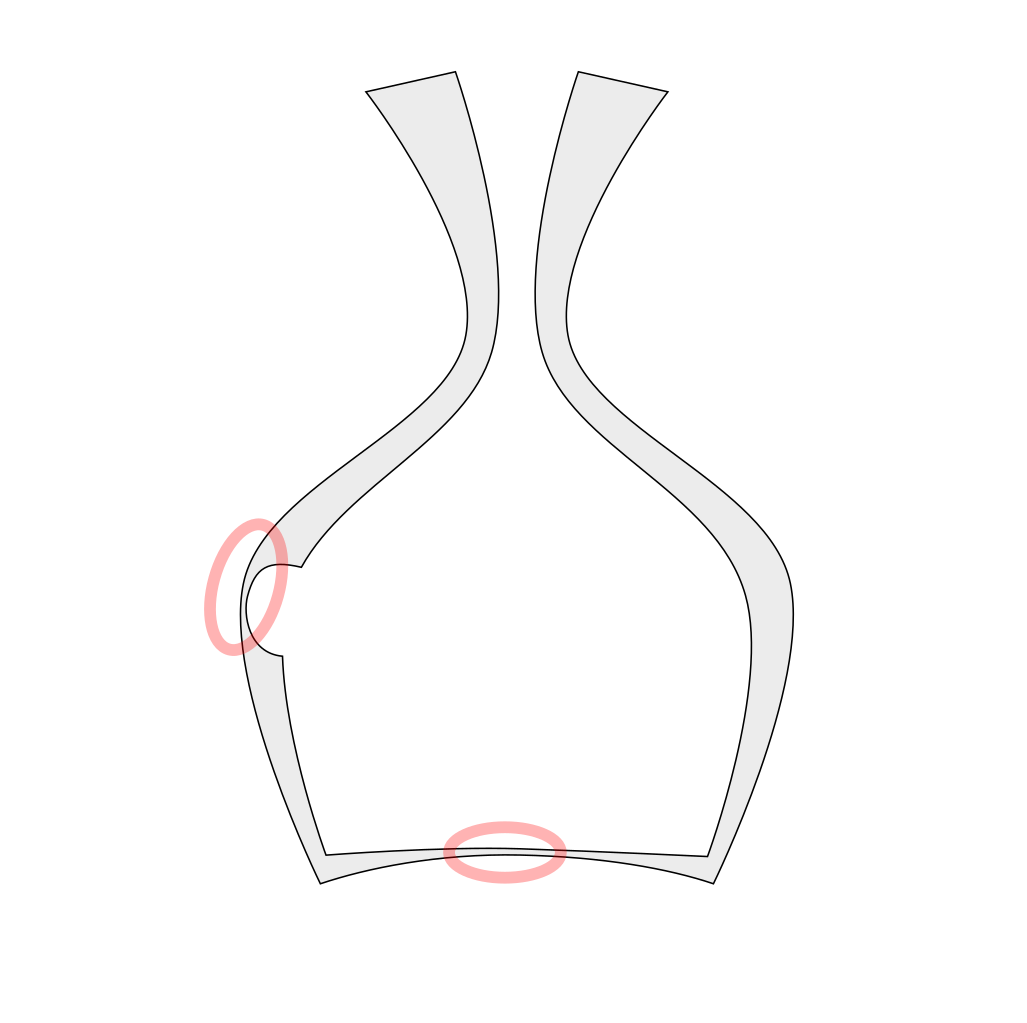La coupe transversale d'un vase met en évidence les problèmes d'épaisseur de paroi
Théoriquement, il est relativement facile de trouver l'épaisseur du modèle en un point particulier, en marchant à l'intérieur du modèle le long de la normale interne jusqu'à ce que nous touchions la surface opposée et que nous quittions le modèle. La distance entre les points d'entrée et de sortie est une bonne approximation de l'épaisseur du modèle à cet endroit.
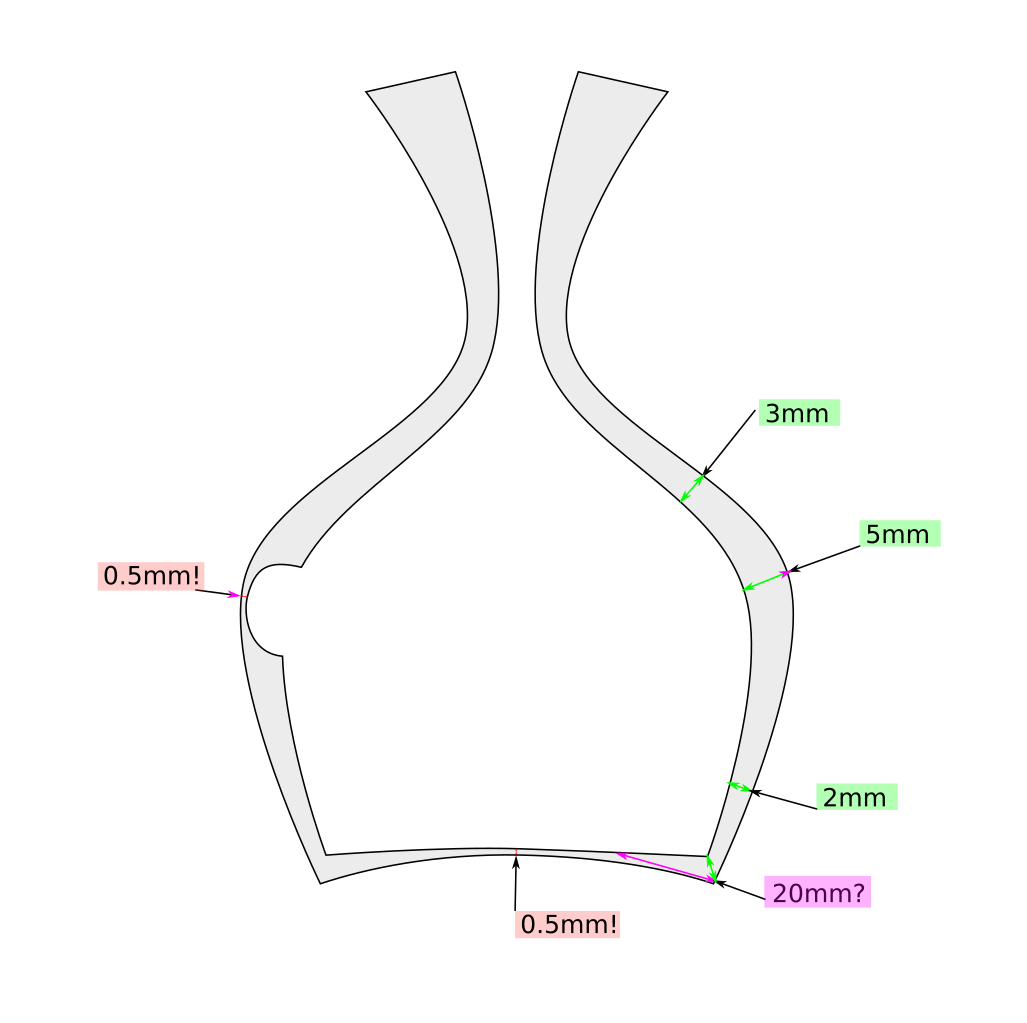Mesure et visualisation naïves et fastidieuses de l'épaisseur des parois
L'examen manuel peut prendre beaucoup de temps. Si vous avez une patience et un temps illimités, cette stratégie pourrait fonctionner. Tous les points sur la surface extérieure du vase dans l'exemple seraient finalement examinés et les régions minces seraient trouvées et identifiées. Ou le feraient-ils?
Une telle approximation de l'épaisseur des objets peut parfois échouer de manière spectaculaire. Dans l'exemple, l'épaisseur de 20 mm en bas à droite de notre vase pose un problème. À cet endroit, la normale interne pointe dans la «mauvaise» direction. Il y a une distance beaucoup plus courte jusqu'au point de sortie indiqué dans la flèche verte. On ne sait pas comment sélectionner la bonne direction à partir du point de départ. Il semble que nous devions analyser toutes les directions à partir du point de départ et sélectionner la direction avec la distance la plus courte. Cela prendrait beaucoup de temps.
Plutôt que cette approche manuelle, une meilleure solution est nécessaire. Nous avons développé un algorithme qui donne tout le travail fastidieux à l'ordinateur et fournit aux utilisateurs une visualisation des régions problématiques.
Définition de la fonction de distance et du calcul du squelette dans les modèles 3D
Tout d'abord, la définition de l'épaisseur de paroi doit être définie à un point particulier. On part de la définition de la fonction de distance signée d'un objet. La valeur de la fonction de distance signée (SDF) en tout point de l'espace est la distance entre ce point et le point le plus proche de la surface de l'objet prise avec un signe négatif à l'intérieur de l'objet et avec un signe positif à l'extérieur de l'objet. L'un des avantages de travailler avec une distance signée est la possibilité de travailler avec les régions intérieures et extérieures de l'objet. La valeur SDF à la surface de l'objet est égale à zéro et elle est approximativement linéaire près de la surface.
Regardons SDF près d'une région avec une paroi mince. Le SDF est fonction de trois variables spatiales (coordonnées x, y, z d'un point) et il faut quatre dimensions pour afficher un tel tracé. Il est plus simple et plus instructif de regarder un graphique de SDF le long d'une ligne unidimensionnelle (un segment). Seules deux dimensions sont nécessaires pour afficher un tel tracé, comme illustré ci-dessous.
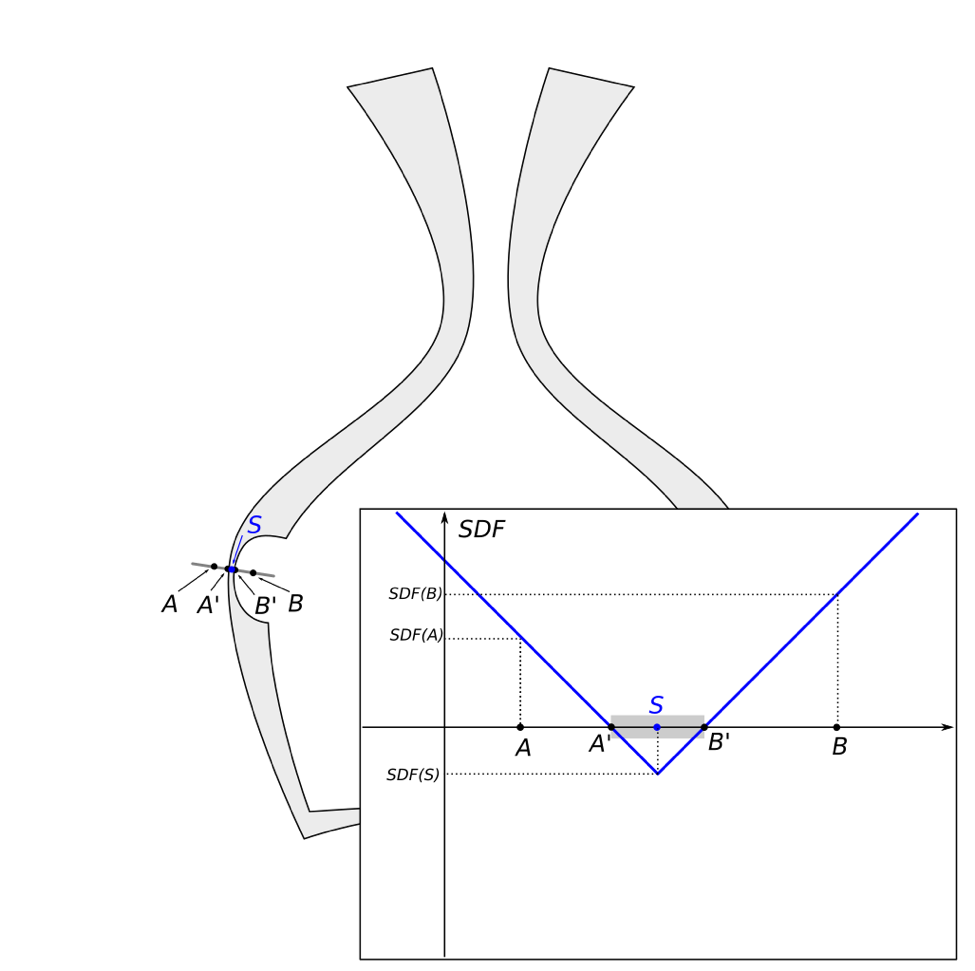Tracé de la fonction de distance signée (SDF) le long du segment AB
Le comportement de SDF le long du segment AB est simple à décrire. Pour les points à l'intérieur de l'intervalle AS, le point le plus proche de la surface de l'objet est le point A 'et le tracé est une simple fonction linéaire – la distance au point A' avec le signe correspondant. Pour les points à l'intérieur de l'intervalle SB, le point le plus proche de la surface de l'objet est B 'et le tracé est une autre fonction linéaire. Le point spécial S est le point à l'intérieur de l'objet qui a des distances égales aux surfaces opposées de l'objet (points A 'et B'). L'ensemble de ces points intérieurs qui ont une distance égale à plus d'un point sur la surface de l'objet est appelé le squelette des objets. Le tracé de SDF près des points du squelette a un minimum net et passe d'une branche linéaire à une autre branche linéaire. Il est clair que SDF (S) – la valeur de la fonction de distance signée au point squelette S est la moitié de la distance entre A 'et B' qui est la définition naturelle de l'épaisseur des objets à cet endroit. Ainsi, nous pouvons définir l'épaisseur de l'objet comme deux fois la valeur absolue de la fonction de distance signée de l'objet au niveau du squelette de l'objet: Thickness = 2 | SDF (S) |. [3]
Ci-dessous, un dessin des points du squelette en couleur.
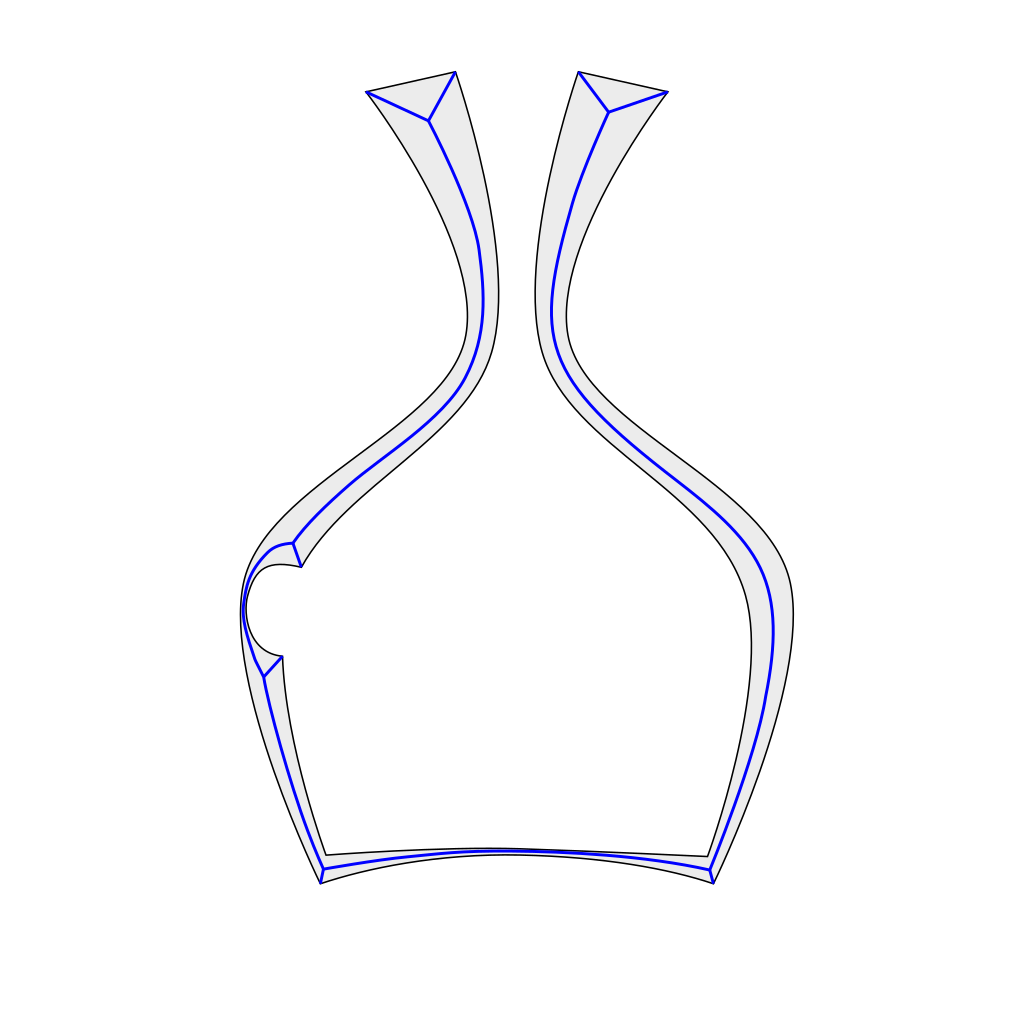Squelette "sale"
Étonnamment, ce squelette a beaucoup de petites branches inattendues (montrées en magenta). Ce sont les points près des bords de l'objet. Ils satisfont tous à la définition du squelette (avec plus d'un point le plus proche sur la surface de l'objet), mais ils sont évidemment sans rapport avec l'épaisseur de l'objet. Si le squelette initial était suivi, la conclusion serait que toutes les régions le long des arêtes vives ont une très petite (zéro) épaisseur. Cette conclusion est clairement insatisfaisante et par conséquent le squelette est appelé un squelette «sale».
Voici les détails du squelette sale près des bords.
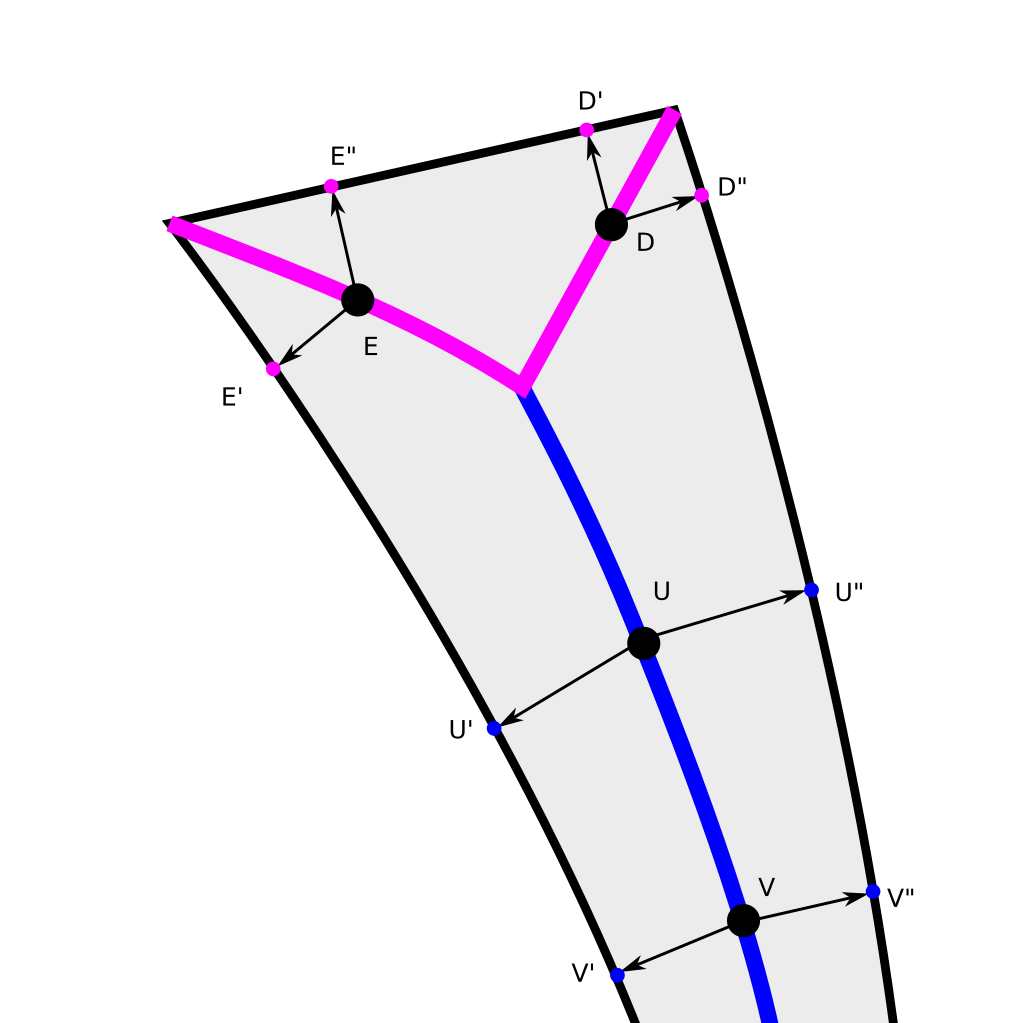Détail du squelette "sale"
Quelques points de squelette sont marqués avec les points correspondants (les plus proches d'eux) sur la surface de l'objet. Les points U et V sont intuitivement de bons points et se trouvent au milieu du mur de l'objet. Les points E et D sont intuitivement de «mauvais» points. Ils correspondent à des arêtes et doivent être ignorés. La différence quantitative entre les cas de bord (E et D) et de mur (U et V) est que ces directions vers les points les plus proches sont presque opposées dans le cas des murs et forment un angle proche de 90 degrés dans le cas du bord. Cet angle peut être utilisé comme critère de seuil pour supprimer les points de squelette de l'arête et ne laisser que le squelette «propre» constitué de points correspondant aux parois de l'objet.
Pour évaluer plus précisément, un squelette «propre» est nécessaire. Voici un exemple du squelette propre pour notre exemple.
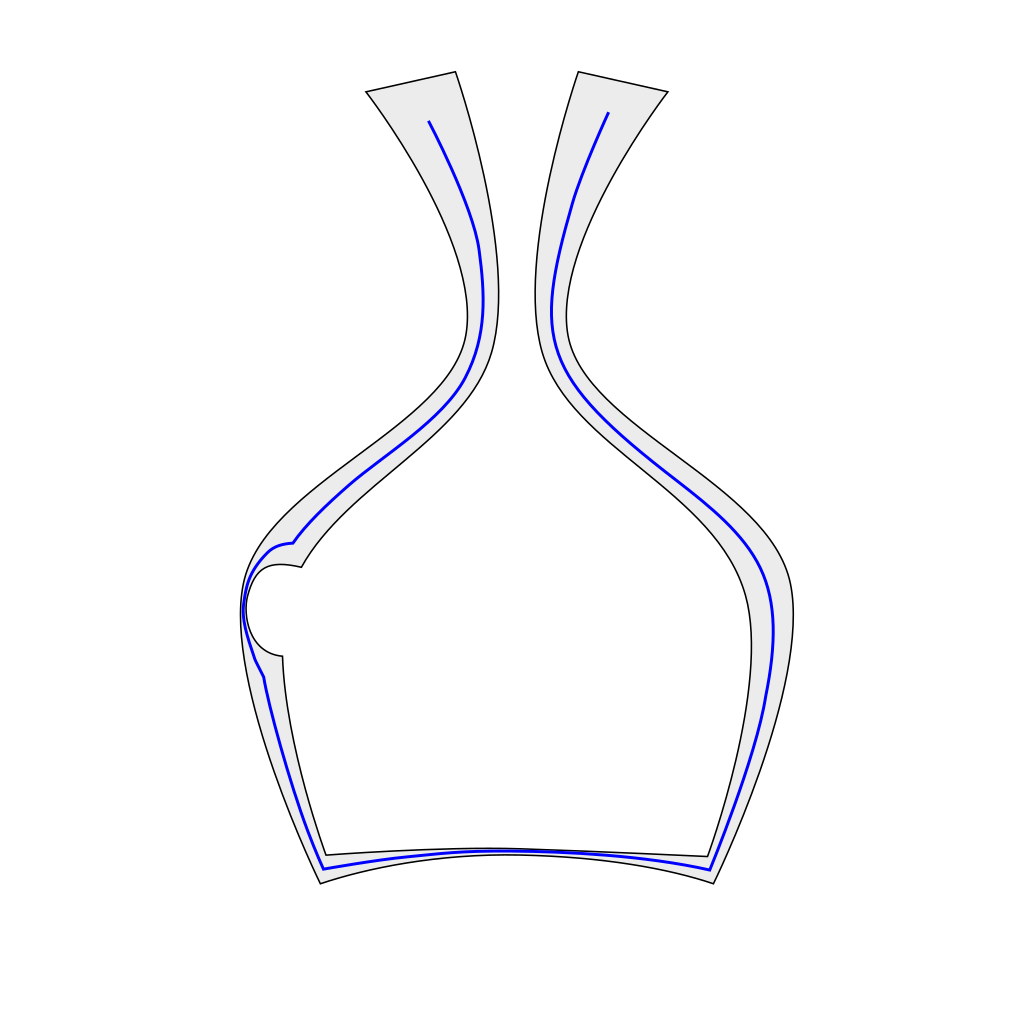Squelette «propre»
Visualisation du squelette et de l'épaisseur de la paroi
Avec le squelette propre, les calculs de parois et d'épaisseur en chaque point ont été déterminés selon le 2 | SDF (S) | formule; cependant, le squelette lui-même peut sembler plutôt peu attrayant, et la relation avec le modèle original peut ne pas être évidente pour un œil non averti. Pour rendre les données du squelette accessibles, nous devons transférer ces informations à la surface du modèle d'origine.
Une façon de faire est de créer un squelette «épais», en visualisant toutes les régions avec une épaisseur de paroi inférieure à l'épaisseur de paroi donnée W. Construire une coque autour du squelette propre avec une épaisseur uniforme W – le squelette épais, sachant que l'épaisseur de la coque est une épaisseur minimale W – partout où la coque est plus épaisse que le modèle, nous pouvons facilement voir un problème d'imprimabilité. Sous toute épaisseur de paroi plus fine que W pose un problème que nous avons mis en évidence en peignant la surface de ces taches en rouge.
Squelette "épais" et régions problématiques
Le squelette peut être utilisé de manière encore plus puissante, en utilisant la fonction de distance au squelette, en mappant la distance à la valeur du squelette en fonction de la gamme de couleurs – en utilisant le rouge comme exemple pour les distances inférieures à l'épaisseur minimale, l'orange pour les distances légèrement plus grandes (par exemple 1,2x mur minimal épaisseur) et vert pour tout ce qui dépasse 1,5 fois l'épaisseur minimale de la paroi. Nous pouvons peindre la surface du modèle original avec des valeurs de distance squelette dans ces couleurs.
Fonction de distance squelette peinte sur le modèle d'origine
La visualisation de l'épaisseur du modèle d'origine est complète, mais simultanément la valeur exacte de l'épaisseur du modèle à un endroit spécifique découle de cette formule simple: Thickness = 2 * DistanceToSkeleton.
Cette procédure complète est utilisée pour créer la visualisation de l'épaisseur de paroi du modèle dans les outils 3D. Il n'est disponible que si l'algorithme a détecté des problèmes d'épaisseur de paroi dans votre modèle.
Visualisation dans les outils 3D
Visualisation de l'épaisseur des parois des outils 3D
Ci-dessus, un exemple d'une telle visualisation d'un modèle problématique. Il s'agit d'une petite pièce mécanique, en acier inoxydable. Ce modèle imprimé dans ce matériau doit avoir une épaisseur de paroi minimale d'au moins 1 mm, mais il y a peu de points où l'épaisseur n'est que de 0,8 mm. Ces taches sont principalement colorées en rouge avec des rayures jaunes le long des limites. Ces points minces se trouvent aux emplacements porteurs de la pièce et sont très certainement les points faibles du modèle, nécessitant la modification du modèle. Il y a peu d'autres endroits où l'algorithme a détecté les parois minces et les a également mis en évidence.
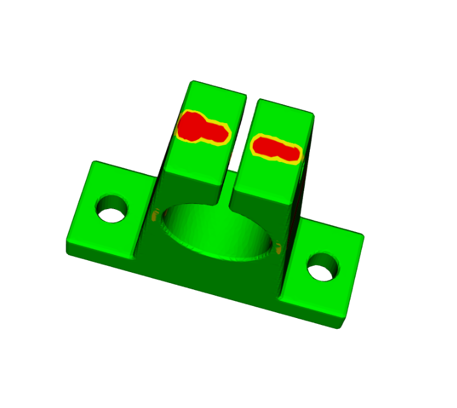
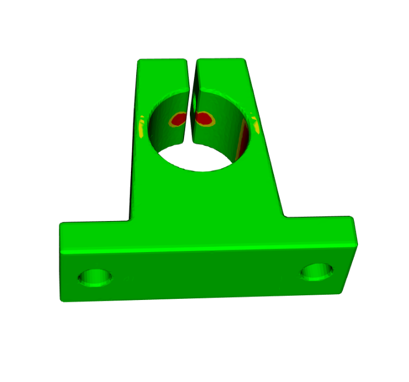
Les points rouges sur ces deux vues ci-dessus sont le long des trous passant sous la surface parallèlement au sommet de la pièce. Ces endroits ne sont pas porteurs et peuvent probablement être ignorés, mais cette décision n'a pas encore été prise par un humain.
En utilisant ce que vous avez appris dans ce blog, vous vous rendrez probablement immédiatement compte que ce modèle a un problème d'imprimabilité. Avec la visualisation, il est plus facile d'analyser et de résoudre le problème d'épaisseur de paroi avant de passer une commande. Le but ultime est de réussir dans l'impression 3D, mais si vous rencontrez toujours des problèmes pour amener le fichier à un état imprimable, les experts en impression 3D de Shapeways sont disponibles pour répondre à vos questions.
Vladimir Bulatov est chercheur en graphisme 3D chez Shapeways, où il se concentre sur les algorithmes d'impression 3D depuis 2012. Outre l'infographie et la modélisation 3D, ses intérêts incluent la physique, les mathématiques et les arts visuels.
Le message Visualiser l'épaisseur de la paroi dans un modèle 3D est apparu en premier sur le blog Shapeways.
